00:00
簡単な言葉で説明できないのなら
あなたは理解していない リチャード・ファインマン
いちです おはようございます
このポッドキャストは僕が毎週お送りしているニュースレター steam news の音声版です
steam news では科学、技術、工学、アート、数学に関する話題をお届けしています
steam news はsteam boat 乗り組みのご協力でお送りしています
冒頭でご紹介したのはノーベル賞物理学者リチャード・ファインマンのsteam な言葉
彼はクリエイティブな天才科学者だったのですが 同時に教えることの名人でもありました
ファインマン先生は本当に本質を理解した結果として 優れたコミュニケーターにもなったんです
さてsteam.fmエピソード116はsteam news 第115号から「資格を四角く並べよう」をお届けします
このエピソードは2023年2月1日に収録しています
僕がポッドキャストをお送りしている理由の一つに 僕自身がポッドキャストを聞くのが好きということがあるんですね
その中でも特にラジオドラマのポッドキャストが好きで
ちょっとでもいい話が聞けると電車の中だろうと歩いている最中だろうと ギャン泣きしてるんです
つい最近聞いたのはというか泣いたのは中心蔵のラジオドラマで
まあ結末もストーリーも知ってるでしょって話なんですが 冒頭のナレーションからブワーって泣いてました
まあ年とともに涙もろくなるのかもしれないですね で中心蔵を聞いていて思い出したのですが
日本の四畳半の和室 これ正方形の和室ですね
ここの畳の並べ方にお作法があるのご存知でしょうか これ上手に並べないと切腹の間というスタイルになってしまうんです
畳の並べ方一つにもお作法を作るところに日本の精神性のようなものをちょっと感じてしまっちゃいますね
このエピソードではこの畳のように四角形の部屋を四角形で埋める問題を取り上げます ただし
信じられないぐらいユニークな方法があるんです 畳は長辺が2
短辺が1の比率の長方形なので2枚一組にすれば正方形になります 畳というのはまあ基本長い辺が六尺短い辺が三尺ですから2枚くっつけると
03:15
6尺6尺 これ一坪という面積になります日本人の生活単位として便利な正方形サイズがまあ一坪ということなんでしょうね
例えば4坪の部屋となるとこれは一坪の正方形を4枚並べればいいことになります まあこれ8畳間がそうなりますよね話が面白くなるのは
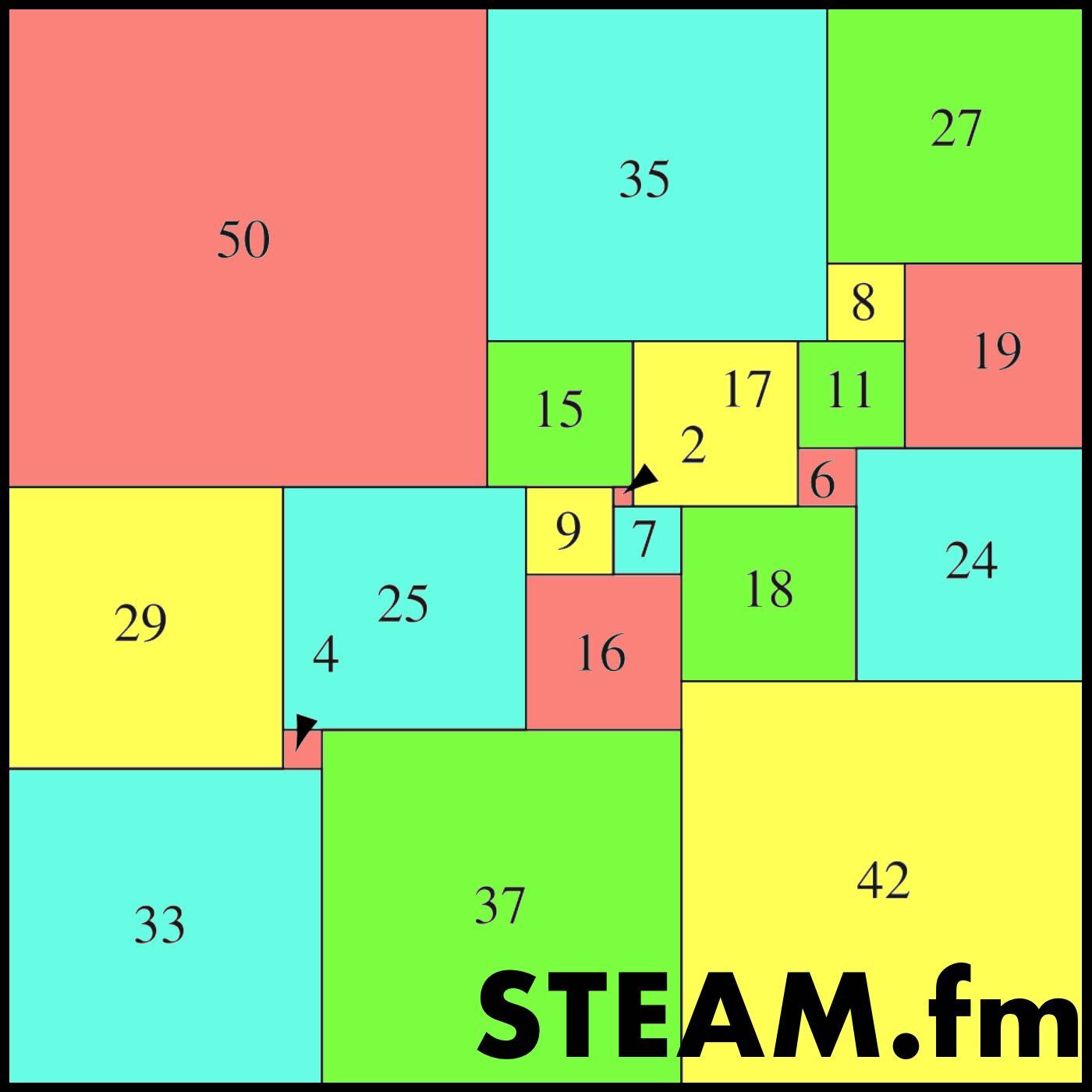
ここからなんです すべてサイズの異なる正方形をきっちりと敷き詰めてより大きな正方形を作ることができるでしょうか
例えて言うならすべてサイズの異なる正方形の畳をきっちりと敷き詰めて より大きな正方形の部屋を作ることはできるでしょうか
この問題は英語でパーフェクトスクエアーどスクエアーと呼びます まあ和訳すると完全なる正方形化された正方形という意味なのですが
英語で正方形化された円 スクエアーどサークルという問題
これ日本語では円積問題という問題があるのですがこれをもじったわけですね 正方形化された円というのはある円と同じ面積を持つ正方形を求めなさいという
こちらは古代エジプト依頼の数学問題で実際古代エジプト人たちはうまい金字を見つけていたんですね この問題をもじってスクエアーどスクエアー
正方形を正方形にしなさい まあ異役すると正方形を敷き詰めて正方形を作りなさいということになります
そんな完全なる正方形化された正方形というのは存在するのかということなのですが 驚くべきことに複数見つかっています
残念ながら音声だけでそのような例をお伝えすることはできないのですが ポッドキャストのカバー画像を見ていただくか
メールでお送りしているニュースレター steam news の本文を見ていただくとそのような例をご覧いただけます ニュースレターへのリンクは概要欄に貼ってありますのでまた良かったら見ていただければと思います
ポッドキャストのカバー画像に使わせていただいた 21個の合い異なる正方形を使って作った正方形
06:00
この正方形は1978年にオランダの計算機科学者 リュージベスティジによって発見されました
しかもこれは最初の完全なる正方形化された正方形ではないんですね 歴史上は24個の合い異なる正方形を使った正方形の方が先に見つかっています
この正方形は1951年にウィルコックスによって発見されました ただこれでもまだ歴史の通過点で
1939年にスプレーグが55個の正方形からなる 完全なる正方形化された正方形を見つけています
こちらが世界で初めて見つかった 完全なる正方形化された正方形でした
本当こんなのよく見つけますよねー っていうか正方形がそれぞれ異なる正方形から作られるというところがもう本当不思議ですよね
合い異なる正方形で正方形を埋めてみようという問いを発したのは ロシアの数学者ニコライ・ルージンでした
彼自身はそんなの無理と思っていたようなのですが このスプレーグがまず最初に回答を見つけたわけですね
ルージンの問題とよく似た問題にミセス・パーキンスのキルトとして知られている問題があります
こちらも正方形をより小さな正方形へと分割する問題なのですが ルージンの問題と違って
同じ正方形が複数回現れても良いものとします ただし小さい正方形の辺の長さはいつも
「互いに素」になっていないといけないんですね この「互いに素」というのは共通の整数で割り切れてはいけないということなんです
こちらもメールでお送りしているニュースレター steam news にその例を挙げていますので よかったら概要欄から飛んで見てみてください
なおこの問題がミセス・パーキンスのキルトと呼ばれる理由なんですが イギリスのパズル作家数学者
ヘンリー・アーネスト・デュードニーがそのように書籍の中で紹介したためなんですね ではなぜミセス・パーキンス夫人なのかとなるとこれは全く不明です
おそらくはキルト作家に女性が多かったので 連想したのかもしれません
デュードニーの死後平面を五角形で敷き詰めるという問題を 数学者ではないキルト作家のミセス・マジョリー・ライスが解いています
09:09
最後にもう一つ面白い幾何学模様の話をしたいと思います ルージンの問題もミセス・パーキンスのキルトも平面をより小さな平面で埋めるという問題でした
一般に無限に広い平面を幾何学図形で埋めていこうとすると必ず繰り返しが現れます
むしろ繰り返すことで無限に埋めていけるような気さえしますよね 100乗間だったら畳を100枚
1万乗間だったら畳を1万枚繰り返し並べていけば敷き詰められるわけです
しかしイギリスの物理学者ロジャー・ペンロースは 菱形2種類を使って繰り返しが現れないパターンを見つけました
この図がペンローズのタイルと呼ばれる 敷き詰めパターンです
どこにも隙間がなくなおかつどこにも繰り返しがないんです 繰り返しがないというのはペンローズのタイルの一部分を切り取って平行移動させても
ピッタリと重なる模様がないということです このような敷き詰めは数学的には非周期タイリングといっていくつも知られています
ペンローズは17世紀の天文学者ヨハネス・ケプラーの仕事から着想を得たとしていますが
ルネサンス記の画家アルブレヒト・デューラーの作品にもヒントが現れていました またこれはですねエッシャーの作品
エッシャー自身は後で述べるイスラム建築から影響を受けていまして このエッシャーの作品を見てペンローズが着想を得たという説もあります
ペンローズご存命なのでもし機会があれば直接聞いてみたいなと思います そのイスラム建築なんですがギリータイルというタイル模様があるんですね
これが非周期タイリングになっているしかもものによってはペンローズのタイルとそっくりのものがあることが現在では知られています
こちらもですねメールでお送りしているニュースレターに実例の写真をご紹介していますので よかったら見ていただけたらなと思います
機科学的な対照性がよく使われる近現代のヨーロッパの建築と一方ですねルールがないのがルールと言われるような日本の禅の美意識の間に 機科学的だけれども周期がないというイスラム美術が位置するのとても面白いと思いませんか
12:09
特にイスラムは偶像崇拝を宗教的に禁止していたためにこういった機科学模様が発展したというふうにも言われています
いや本当今回お送りした内容はこのグラフィックで見ていただかないとしょうがないので ぜひあの無料でお読みいただけますので
ニュースレター steam news ご登録いただいて バックナンバーは web で読めますので見ていただければなと思います
写真とか絵の部分だけでもね見ていただけると面白いかなと思います というわけでこのエピソードでは資格を資格く並べようという話をお届けしました
このエピソードを2023年2月の頭に収録しているのですが ベブサイトサイエンスニュースが2023年に訪れるべき
7つの新しいサイエンスミュージアムという特集記事を掲載していましたのでご紹介してみたいと思います 7つの新しいサイエンスミュージアムなのですが
その第1弾がですねエジプトの グランドエジプシアンミュージアム
通称GEMですね G E Mで GEM 日本語では大エジプト博物館というふうに
呼ばれています 2023年
オープン これ
ただまだあの去年からですねオープンするぞオープンするぞっていう話を聞いていたんですが まだオープンしていないので今年こそオープンしてくれという感じの
グランドエジプシアンミュージアム 僕もすごく行きたいです 建築現場はね何度も横通っているんですがなかなかオープンしないので早く行きたいです
2番目リチャードギルダセンター for science education and innovation
これはニューヨークシティにあります 150年以上の歴史を持つアメリカンミュージアムオブナチュラルヒストリーに新しく
設備が導入されて 写真で見るとですねなんかこうバーチャルリアリティを体感できるような没入型の展示スペースのように
なっているようです 3つ目
ガラパゴスアイランド まあといってもこれガラパゴス諸島に行くわけではなくてヒューストンにあるそうです
テキサスのヒューストンですね これはガラパゴストを再現した
ような 博物館になっています
15:02
4番目 カンザスシティズアクエリアム カンザスシティ
動物園水族館 これも2023年の9月にオープンするそうなんですが
カンザスシティですからねこれ水売り州ですかね ちょっと日本から行くには遠いかもしれないのですがまぁアメリカに行く用事があれば
ちょっとワンホップして いけるのかなぁと思います
5番目 スペースフランクリンインスティチュート
フィラデルフィアにあるそうです こちらは宇宙開発に特化した博物館だそうで将来のテクノロジーは宇宙で住んでいくために必要な
テクノロジーなんかも紹介してくれているそうです これも個人的にはですねすごく行ってみたい
博物館ですね 6つ目バードハウススミソニアンズナショナルズということでこれは
ワシントン dc 首都のワシントン dc にある 鳥類の鳥の動物園ということですね
そして7番目 ロボット&ai ミュージアム
ソウルというわけでこれはですね韓国ソウルにできる ロボット&ai ミュージアムこれまだね必オープンなのか正式なアナウンスはないようなのですが
まあ ai とロボットの博物館まあそれ専門の博物館ということでこちらは日本からも近いので まあソウル遊びに行くよという人はね検討されてみてはいかがでしょうか
個人的にはですねまぁいくつも気になる場所あるのですがもちろんジェムはちょっと別格であの大 エジプト博物館ですねこれあの
多分あのツタンカーメンなんかも移動すると思うのでこれ別格ですごく気になってるんですけれども6番目の ワシントン dc のバードハウスですね
こういった動物でてやっぱり地域ごと施設ごとにすごく特徴というのが出てくるので まだ詳細はねわからないのですがまあどういった
鳥さんたちを展示展示というかあのまあ動物なのでねあの飼育するのかっていうのは すごく興味があります
僕の住む長崎では長崎ペンギン水族館というね あのペンギンを飼ってる水族館がいてあの昼になるとペンギンがね
海辺にあの遊びに行くんですよそれをあの一緒にね ペンギンと一緒にこう歩いて海まで行けたりとかするっていうね
18:01
でどうもここの長崎にしかあの飼育されてない ペンギンがいるそうなので僕もちょっとペンギンの種類わかんないんですけども
全国からね日本全国からペンギンファンの方が来られるそうです あとまあ長崎バイオパークっていうこれも長崎市内からちょっと離れた
最開始というところにあるんですがここのね バードハウスもあのコウモリとかいてコウモリってね
あの近くで見るとすごく近くで見れるんですけれども ああやっぱり哺乳類なんだってねなんか妙に感動したりとかするので
ぜひこういうね動物園であったりとかバードハウスであったりとか水族館なんかもそれぞれ あの特徴がね出てきますので
まあ直接あの訪問できなくてもまあウェブサイトなんかで見ていくだけでも楽しいかなと思います おすすめです
では番組最後にニュースレターの宣伝です ニュースレターではですねまあ今日お届けした内容の
他に今週の書籍今週のテッドトークもご紹介していますそれからね q & a とまあ編集後期に位置づけている
1510の話というのもお届けをしています 今週の書籍は
とてつもない数学という書籍なのですがこの本の第3章に応える色詰め問題も紹介されています これねとてもね面白い本でまたまだねあのご紹介したいネタがたくさん詰まっていたので
またこの steam.fm でもオリに触れてご紹介していきたいと思っています 今週のテッドトークのコーナーでは正確に言うと
テッドではなくててど x の方ですねてど x の方のトークをご紹介しているのですが
tdx 東京からちょうどですね10年前11年前ですね2012年の トーク
ハブ吉原9弾のてデックストークをご紹介しています 実はですねこのトークまああの今 youtube で
アップされていて見ることができるのですがこのステージ裏であの僕オペレーションしていたんです あの
次のスピーカーはハブ吉原さんですってこう cg でねあの画面を送って で彼は確か3枚だけ写真を使われたんですよ
でまぁその写真を舞台裏からお送りしたりとかして なんかの彼ハブさんとってもいい人でした
なんかこうプロの将棋の騎士の方って変わった方が多い印象があるじゃないですか まあ変わった方が特に印象深いからみんなそうだと思いがちなのかもしれないですがハブさんは
21:11
大変常識的な方でした もちろんねあの
将棋を刺される時はもう すごい天才なんでしょうけれども
接不断こうね接してくださる分にはとても 真摯的で穏やかな方でした
ニュースレターではそんなハブさんのトーク youtube への音リンクなのですがご紹介をさせていただいています
今週の q&a なのですがこれもねちょっとニュースレターでお送りしてよかったのかどうか 迷ったんですがこんな q&a をお届けしました
恋人に二股をかけられたことはありますか どのような気分でしたかという内容で
いやこれニュースレターに文字としてお答えはしたんですが改めて口頭で 答えするのは恥ずかしいですね
あの僕ですね二股というか3つ股かけられていたことがありまして でどう思ったかっていうと誇らしく思ったんですよあ俺すげーと思ったんですよ
なんかほらこう男3人と同時に付き合えるスーパーウーマンとを付き合いできるなんて いやなんて光栄なんだろうと思ったんですよ
でしかもですね彼女の残り2人の恋人たちにもお会いしたんです そしたらねもうねめちゃくちゃいい男で
いやもうなんかラインナップに加えていただいてもありがとうございますって感じで ちょっと花高いぜと思ったんですけれども
いや僕おかしいですかねちょっと言ってて恥ずかしくなってきました まあそんなあの
こともニュースレターでお届けをしています 言っちゃった
ん
このポッドキャストではコーヒーの差し入れも受け付けております 無料放送を維持するためによかったらの400円からご支援いただけますのでご検討
いただければ幸いです 大変熱かましいお願いなのですが
概要欄にコーヒーの差し入れのリンクがありますのでまあよかったらご検討くださいませ
というわけで今週も最後まで聞いてくださってありがとうございました これを機にアートと数学の関係について思いを馳せていただけると嬉しいです
お相手はsteam.fm の1でしたではまた次のエピソードでお会いしましょう
24:02
2 サーフェイプ2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2